二瓦計和三瓦計應用區別

一、概述

在三相電路的功率測量中，主要測量方法有二瓦計法和三瓦計法兩種方法。對于不同的接線方式場合，應選擇恰當的功率測量方式，才能得到準確的功率參數。但是由于部分使用者對于這兩種方法適用的場合不夠清晰，因此在選擇二瓦計或者三瓦計法進行三相功率測試時，極易造成混淆，從而導致選擇了錯誤的測量方法。

那么究竟在什么樣的情況下使用兩瓦計法，什么樣的情況下采用三瓦計法進行三相功率的測量呢？本文從三相電路功率測量的原理角度下分析這兩種方法的異同以及分別適用的場合。

二、二瓦計法

1、測量原理

二瓦計法的理論依據是基爾霍夫電流定律，即：在集總電路中，任何時刻，對任意結點,所有流入流出結點的支路電流的代數和恒等于零。也*是說，兩根火線的流入電流等于第三根火線的流出電流，或者說，三根火線的電流的矢量和等于零，即：

　　i_a+i_b+i_c=0　　（1）

　　假設三相負載的中線為N，依據電壓的定義：

　　u_ab=u_an-u_bn，u_cb=u_cn-u_bn　　（2）

三 相瞬時功率：

　　p=u_an*i_a+u_bn*i_b+u_cn*i_c，　　（3）

　　將式（1）和式（2）代入式（3），得：

　　p=u_an*i_a+(-u_bn*i_a+u_bn*i_a)+u_bn*i_b+u_cn*i_c

　　=u_ab*i_a+u_bn(i_a+i_b)+u_cn*i_c

　　=u_ab*i_a+u_bn(-i_c)+u_cn*i_c

　　=u_ab*i_a+u_cb*i_c。

有功功率等于瞬時功率在一個周期內求積分再求平均，得到：

　  P=P₁+P₂

　  P為三相電路有功功率的總和，P₁為u_ab*i_a在一個周期內的積分的平均值，P₂為u_cb*i_c在一個周期內的平均值。在正弦穩態電路中：

　  P=U_AB*I_A*cosφ_AB+U_CB*I_C*cosφ_CB

　  即：P₁=U_AB*I_A*cosφ_AB   P₂=U_CB*I_C*cosφ_CB

    式中，U_AB、I_A、U_CB、I_C均為正弦電壓電流的有效值，φ_AB為U_AB和I_A的相位差，φ_CB為U_CB和I_C的相位差。

從變換的公式中可以看出，采用這種方法進行三相總功率測量時，只需要測量兩個電壓和兩個電流，這*是二瓦計法的推導原理及由來。

二瓦計法測量時，三相電路總功率等于兩塊功率表的功率之和，每塊功率表測量的功率本身無物理意義。

2、接線方法

二瓦計法接線示意圖如下所示（以測量UabIa，UcbIc為例）：

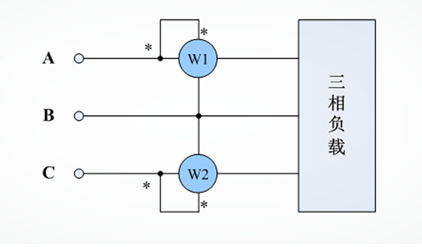
圖1.二瓦計法功率表接線示意圖

圖1中，單相功率表或三相功率表的某一相W1測量的是P₁=U_AB*I_A*cosφ_AB，W2測量的是P₂=U_CB*I_C*cosφ_CB。則三相電路總功率為：P=P₁+P₂。

3、適用場合

由于二瓦計法的理論依據是基爾霍夫電流定律，適用于在三相回路中只有三個電流存在的場合，如：

1、 三相三線制接法中線不引出（只能采用兩瓦計法）；

2、 三相三線制接法中線引出但不與地線或試驗電源相連的場合，與是否三相平衡無關。

三、三瓦計法

1、測量原理

三瓦計法需要將中性點做為電壓的參考點，分別測量出三相負載的相電壓，相電流，那么三相電路的總功率為三個單相電路的功率之和，每塊功率表測量的功率*是單相功率。

如果以瞬時值表示的話，即：

　p_a=u_a*i_a，p_b=u_b*i_b，p_c=u_c*i_c，

那么三相瞬時功率：

　p=p_a+p_b+p_c，

則三相總有功功率為：

　P=P_A+P_B+P_C

在正弦穩態電路中，

　P_A=U_A*I_A*cosφ_A

　P_B=U_B*I_B*cosφ_B

　P_C=U_C*I_C*cosφ_C

　其中φ_A、φ_B、φ_C分別為U_A與I_A、U_B與I_B、U_C與I_C的相位差角。

2、接線方法

三瓦計法測量接線示意圖如下所示：

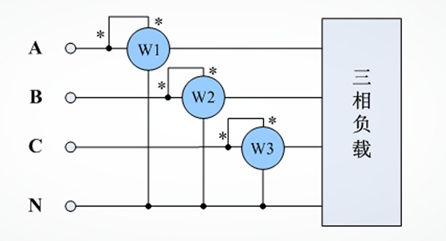
三瓦計法功率表接線示意圖

3、適用場合

三瓦計法由于需要采用中性點作為電壓的參考點，因此適用于如下場合選用：

1、 三相三線制中性線引出，但中性線不與電源或地線連接的場合；
2、 三相四線制，由于無法判斷三相負載是否平衡或是否在中性線上有零序電流產生，只能采用三瓦計法；

四、誤區

1、誤區一

二瓦計法只適合于三相對稱電路的功率測量。
這種說法顯然是不正確的。

首先，二瓦計法的證明中，只有i_a+i_b+i_c=0的假設，并沒有要求三相對稱。

其次，如果三相負載完全對稱，那么只需要一個功率表（比如P_A）即可得出三相總功率，即P=3P_A，二瓦計法也失去了意義。

2、誤區二

用二瓦計法測量三相四線制的總功率。
由于三相四線制有四個電流（i_a、i_b、i_c和i_n），而二瓦計法依據的是基爾霍夫電流定律，在三相回路中，三相電流矢量之和必須等于零。但是在三相四線制回路中，會產生零序電流分量，這*使得i_a+i_b+i_c≠0，因此，二瓦計法不適用三相四線制的總功率測量，三相四線制系統應采用三瓦計法。